Curso Finanzas para Vendedores
Capítulo 1: Los porcentajes
El conocimiento y el manejo de los porcentajes es una habilidad esencial que deben tener los vendedores de cara a alcanzar acuerdos comerciales fructíferos. A menudo, muchos vendedores sólo saben calcular el porcentaje con su calculadora aplicando la tecla % más o menos, según las circunstancias. Sin embargo, para desarrollar sus funciones comerciales con éxito, los vendedores necesitamos comprender en profundidad el concepto de porcentaje, así como aplicar los diferentes cálculos de porcentajes.
En la actividad comercial diaria empleamos los porcentajes en los descuentos comerciales, en la construcción del precio neto de venta, en la aplicación de los impuestos, en la negociación de las condiciones de los diferentes acuerdos, en el cálculo de los márgenes, en la arquitectura de los costes, en las diferentes operaciones financieras y en un largo etcétera.
Comenzaremos el presente curso de finanzas para vendedores desarrollando en profundidad el concepto de porcentaje, así como los diferentes cálculos de porcentajes y sus aplicaciones en el área comercial.
Significado del porcentaje
El porcentaje es un tanto por cien o por ciento. El símbolo matemático que se emplea es “%”.
Un porcentaje es una forma de expresar un número como una fracción de 100. “Por cien” o “por ciento” significan “de cada 100”. El porcentaje es una cantidad que corresponde proporcionalmente a una parte de cien.
Con un ejemplo entenderemos mejor el significado de un porcentaje. Para calcular el 10% de una cantidad: de cada “100” elementos, unidades o cosas que una forman una cantidad, consideramos “10” elementos, unidades o cosas. El punto de partida es la cantidad y de cada 100 elementos de dicha cantidad, tomamos 10.
El 10% de 100 euros, es tomar 10 euros de cada 100 euros. Como sólo hay 100 euros, tomamos 10 euros.
El 10% de 400 euros, es tomar 10 euros de cada 100 euros. Hay 4 grupos de 100 euros (4 grupos x 100 euros = 400 euros). De cada grupo de 100 euros, tomamos 10 euros y como hay 4 grupos, el resultante es 40 euros (4 grupos x 10 euros = 40 euros).
El 10% de 200 productos, es tomar 10 productos de cada 100 productos. Hay 2 grupos de 100 productos. De cada grupo de 100 productos, consideramos 10 productos y como hay 2 grupos, el resultante es 20 productos (2 grupos x 10 productos = 20 productos).
Cálculo de porcentajes
El cálculo de porcentajes se puede realizar siguiendo los siguientes métodos:
- Método de la regla de tres simple
- Método de la fracción
- Método del índice.
1. Cálculo del porcentaje mediante regla de tres simple
Procedemos a calcular el 10% de 300 euros mediante la regla de tres simple. Si tengo 100 euros, debo tomar 10 euros y si tengo 300 euros debo tomar “x” montando una regla de tres simple.
100 euros => 10 euros
300 euros => x
Para resolver la regla de tres simple, multiplicamos en cruz e igualamos la ecuación resultante:
100 euros por x = 300 euros por 10 euros
100 * x = 300 * 10
Despejamos la ecuación para calcular la x, llevándonos los 100 euros de la izquierda de la ecuación al lado derecho de la misma dividiendo:
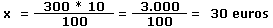
De igual forma, calculamos el 15% de 60 euros montando la regla de tres simple, tomando 15 euros de cada 100 euros:
100 euros => 15 euros
60 euros => x
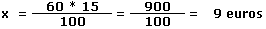
El cálculo de porcentajes mediante una regla de tres simple es muy sencillo y resulta demasiado infantil. Por ello, aconsejamos que se utilicen los siguientes métodos que estudiaremos a continuación.
2. Cálculo del porcentaje mediante una fracción
Para calcular el 10% de una cantidad aplicando el método de la fracción recurriremos a la definición de porcentaje. De cada 100 unidades, tomamos 10 y lo multiplicamos por la cantidad. Dicho de otra forma, multiplicamos 10 por la cantidad y lo dividimos entre 100. De esta forma obtenemos la fracción que nos permita calcular el porcentaje:

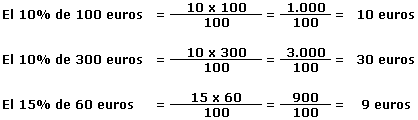
3. Cálculo del porcentaje mediante un índice
El método del índice es el método que os recomendamos para calcular porcentajes. A partir de las fracciones vistas anteriores, obtenemos el índice que utilizaremos para calcular un porcentaje.
Para calcular el 10% de una cantidad, multiplicamos 10 por la cantidad y dividimos por 100. Montamos la fracción de una forma diferente, dividiendo 10 entre 100 y multiplicamos por la cantidad. El índice del porcentaje es 10 dividido entre 100, es decir, “0,1”. Para calcular 10% de una cantidad, multiplicamos dicha cantidad por el índice “0,1”.

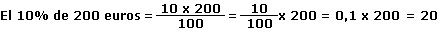
Para calcular el porcentaje de una cantidad, partimos del índice de dicho porcentaje y los multiplicamos por la cantidad. El índice de un porcentaje es dividir dicho porcentaje entre 100. El índice del 10% es 10 dividido entre 100, es decir, “0,1”.
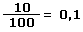
Para calcular el porcentaje multiplicamos el índice por la cantidad:
10% de 200 euros = 0,1 x 200 = 20 euros
Averigüemos el 15% de 60 euros mediante el método del índice. Primero obtenemos el índice del 15% que es 0,15 (15 dividido entre 100). Finalmente, multiplicamos el índice 0,15 por la cantidad.
15% de 60 euros = 0,15 x 60 = 9 euros
A continuación mostramos más ejemplos, calculando el índice del porcentaje y multiplicamos por la cantidad:
8% de 200 euros = 0,08 x 200 = 16 euros
20% de 30 euros = 0,2 x 30 = 6 euros
5% de 20 dólares = 0,05 x 20 = 1 dólar
Aumentos porcentuales
Los aumentos porcentuales sirven para sumar a una cantidad inicial el incremento que le supone un determinado porcentaje.
Este cálculo es muy útil para calcular el precio final de un artículo sumándole la cantidad del impuesto del valor añadido (IVA). Imaginemos un artículo que cuesta 250 euros sin IVA y queremos obtener su precio final teniendo en cuenta un IVA del 18%.
El método más sencillo es calcular cuánto supone dicho porcentaje y sumarlo a la cantidad inicial. Siguiendo con nuestro ejemplo, calculamos el 18% de 250 euros y se los sumamos.
18% de 250 euros = 0,18 x 250 = 45 euros
Precio final = 250 euros + 45 euros = 295 euros
Otra forma de calcular los aumentos porcentuales es empleando los índices de variación del aumento porcentual. Partiendo del índice de un porcentaje le sumamos 1 y multiplicamos por la cantidad inicial, obteniendo la cantidad final tras el aumento porcentual.
Siguiendo con el ejemplo del artículo cuyo precio sin IVA es 250 euros y el IVA corresponde al 18%, calcularemos la cantidad final con el IVA incluido. Partimos del índice porcentual del 18%. Recordemos que el índice porcentual es dividir el porcentaje entre 100. El índice porcentual del 18% es 0,18. Sumamos 1 a este índice porcentual. Multiplicamos la cantidad inicial por 1,18, siendo el resultado 295 euros.
1 + 0,18 = 1,18
250 x 1,18 = 295 euros
Esta forma de calcular los aumentos porcentuales siguiendo el índice de aumento porcentual es el que te recomendamos que uses habitualmente.
Veamos otro ejemplo para aprender este método. Imaginemos que compramos una materia prima a 300 euros y de repente sube un 8%. ¿Cuál será el precio final de la materia prima tras la subida? Primero calculamos el índice de porcentaje de 8% que es 0,08 (8 dividido entre 100). A continuación sumamos 1 a este índice, resultando 1,08. Finalmente multiplicamos el precio inicial 300 por 1,08 y obtenemos un precio final tras la subida del 8% de 324 euros.
1 + 0,08 = 1,08
300 x 1,08 = 324 euros.
Supongamos que ganamos 1.500 euros y nos suben el salario un 5%. ¿Cuál será el nuevo salario tras la subida del 5%? Igual que en los ejemplos anteriores, calculamos el índice de porcentaje de 5% que es 0,05 (5 dividido entre 100). A continuación sumamos 1 a este índice, resultando 1,05. Finalmente multiplicamos el salario inicial 1.500 por 1,05 y obtenemos el nuevo salario tras la subida del 5% de 1.575 euros.
1 + 0,05 = 1,05
1.500 euros x 1,05 = 1.575 euros
Disminuciones porcentuales
Las disminuciones porcentuales se utilizan para obtener el resultado final de una cantidad de la cual le restamos un porcentaje. De igual forma que calculamos los aumentos porcentuales, resolveremos las disminuciones porcentuales aplicando los índices de variación de la disminución porcentual.
En el caso de las disminuciones porcentuales, el resultado final se obtiene restando a 1 el índice porcentual y multiplicando por la cantidad inicial. Vemos este concepto con un ejemplo.
Supongamos el precio de un artículo en una tienda sufre un descuento del 10%, siendo el precio inicial 200 euros. ¿Cuál será el precio final tras aplicarle el descuento? Partimos del índice porcentual del 10%. Recordemos que el índice porcentual es dividir el porcentaje entre 100. Tal como hemos visto anteriormente el índice porcentual del 10% es 0,1. Restamos 1 a este índice porcentual. Finalmente multiplicamos la cantidad inicial por 0,9, siendo el resultado 180 euros.
1 – 0,1 = 0,9
200 x 0,9 = 180 euros
Para profundizar en el concepto de las variaciones porcentuales vamos a desarrollar otro ejemplo. Supongamos que un producto cuesta 150 euros y está promocionando la compra de una segunda unidad de dicho artículo con un 70% de descuento. ¿Cuánto nos costaría comprar la segunda unidad de dicho producto promocionada? La resolución es tan fácil como aplicar el método de las variaciones porcentuales. La primera unidad vale 150 y la segunda unidad tiene un descuento del 70%. El índice porcentual del 70% es 0,7 (70 dividido entre 100). Restamos a 1 ese índice porcentual, obteniendo 0,3. Multiplicamos 0,3 por el precio inicial y el resultado es 45 euros. El precio de la segunda unidad promocionada es 45 euros.
1 – 0,7 = 0,3
150 x 0,3 = 45 euros
Casos especiales
A continuación vamos a estudiar varios casos especiales relacionados con los porcentajes.
1. Aumentos y disminuciones consecutivos
Imaginemos que el precio inicial de una acción de una empresa que cotiza en bolsa es de 300 euros. El primer día el precio sube un 10% y el segundo día el precio baja otro 10%. ¿Cuál es el precio de la acción al cierre del segundo día? Inicialmente, responderíamos que el precio continúa siendo 300 ya que sube el primer día un 10% y baja otro 10%. Sin embargo, ese resultado es erróneo ya que las bases sobre las cuales calculamos el incremento y la disminución porcentuales son distintas. Vemos como resolvemos correctamente a esta pregunta.
El primer día la acción se incrementa un 10% el precio. Aplicamos el método del aumento porcentual. El índice del 10% es 0,1. Sumamos 1 a este índice y obtenemos 1,1. Multiplicamos 1,1 por el precio inicial y obtenemos el precio al final del primer día que es 330 euros.
1 + 0,1 = 1,1
300 x 1,1 = 330 euros precio de la acción al cierre del primer día
El segundo día la acción se deprecia un 10%. Aplicamos el método de la disminución porcentual. El índice del 10% es 0,1. Restamos 1 a este índice y obtenemos 0,9. Multiplicamos 1,1 por el precio de cierre del primer día y obtenemos el precio al final de cierre del segundo día que es 297 euros. Este es el resultado correcto.
1 – 0,1 = 0,9
330 x 0,9 = 297 euros precio de la acción al cierre del segundo día
2. Calcular la cantidad inicial con aumentos porcentuales
En ocasiones, conocemos la cantidad final una vez que se ha aplicado un determinado aumento porcentual. Pero, ¿cómo podemos calcular la cantidad inicial?
Como hemos estudiado con los aumentos porcentuales, la cantidad final es igual a la cantidad inicial multiplicada por 1 más el índice porcentual.
Cantidad final = cantidad inicial x (1 + índice porcentual)
Despejando en la ecuación obtendremos la cantidad inicial que es igual a la cantidad final divida entre 1 más el índice porcentual. La fórmula es la siguiente:
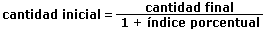
Veamos este cálculo con un ejemplo. Supongamos que un producto incluido ya el IVA del 18% cuesta 295 euros. ¿Cuál es su precio inicial sin tener en cuenta el IVA del 18%? Es un problema de cálculo de cantidad inicial, conociendo la cantidad final. La cantidad final es el precio con IVA incluido, es decir, 295 euros. El índice porcentual del 18% es 0,18 (18 dividido entre 100). Para calcular el precio sin IVA aplicamos la fórmula que hemos visto anteriormente.

El precio inicial sin IVA es 250 euros. Si le aplicamos el 18%, el precio con IVA es de 295 euros.
3. Calcular la cantidad inicial con disminuciones porcentuales
Podemos conocer la cantidad final una vez que se ha aplicado una determinada disminución porcentual. Pero, ¿cómo podemos obtener la cantidad inicial?
Como hemos visto con las disminuciones porcentuales, la cantidad final es igual a la cantidad inicial multiplicada por 1 menos el índice porcentual.
Cantidad final = cantidad inicial x (1 - índice porcentual)
Despejando en la ecuación hallaremos la cantidad inicial que es igual a la cantidad final divida entre 1 menos el índice porcentual. La fórmula es la siguiente:
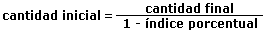
Desarrollemos este cálculo con un ejemplo. Imaginemos que un determinado artículo cuesta 180 euros una vez que le han aplicado un descuento del 20%. ¿Cuál es su precio inicial antes de disminuirlo con el 20% de descuento? Es un problema de cálculo de cantidad inicial, conociendo la cantidad final. La cantidad final es el precio con el descuento del 20%, es decir, 180 euros. El índice porcentual del 20% es 0,2 (20 dividido entre 100). Para calcular el precio inicial antes del descuento aplicamos la fórmula que hemos visto anteriormente.

El precio inicial sin descuento del 20% era de 225 euros. Si le aplicamos el 20% de descuento, el precio final es de 180 euros.
4. Cálculo del porcentaje partiendo de la cantidad inicial y la cantidad final
Para calcular cuál es el porcentaje de incremento partiendo de la cantidad inicial y la cantidad final, empleamos la fórmula del aumento porcentual.
Cantidad final = cantidad inicial x (1 + índice porcentual)
Despejamos de la ecuación el índice porcentual y lo multiplicamos por 100 para obtener el incremento porcentual. Resumiendo, aplicamos la siguiente fórmula.

Mediante un ejemplo comprenderemos mejor este cálculo. Si un artículo costaba 80 euros y ahora vale 120 euros, ¿cuál ha sido su incremento porcentual del precio? Para solucionar esta pregunta aplicamos la fórmula anterior.
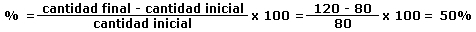
Como podemos ver el artículo ha incrementado su precio un 50%.
Ejercicios
Ejercicio número 1: Calcula cuánto es el 30% de 300 euros.
Ejercicio número 2: ¿Cuál es el índice de porcentaje del 50%?
Ejercicio número 3: Si el precio del petróleo sube un 15% desde los 70 dólares barril, ¿cuál es el nuevo precio del barril de petróleo?
Ejercicio número 4: Si un artículo que costaba 20 euros, se rebaja un 25%, ¿cuál es el nuevo precio del artículo?
Ejercicio número 5: Si una materia prima que costaba 120 dólares por kilo, sube durante el primer mes un 15% y desciende un 20% el precio durante el segundo mes, ¿cuál es su precio final al término del segundo mes?
Ejercicio número 6: Si una barra de pan cuesta 52 céntimos de euro con un IVA incluido del 4%, ¿cuál es su coste sin IVA?
Ejercicio número 7: Calcula cuál es el incremento porcentual del coste de un artículo que costaba 200 euros y ha incremento su precio hasta 225 euros.
Ejercicio número 8: ¿Cuál es la tasa porcentual de ocupación de un hotel con 200 habitaciones en total y 40 habitaciones sin ocupar?







